do i=-lhwidth,lhwidth
xt=dfloat(i)/hw
xv=(dcos(dpi/2.d0*xt))**2
& *( (dcos(dpi*xt))**2
& - (cos(dpi*(dabs(xt)-0.5d0)))**2 )
x(i)=xt
enddo
TSF EDIT 600One can show that the 10+60 sequence is optimum for 1-to-600 decimation
REPAIR L<=10
FILTER D:WD KAIS 40 2.1 0.0 0.05 0.5 0.0
DECIMATE 10 ${MOVE} 0
FILTER D:WD KAIS 58 2.1 0 0.0333 1.0 0.0
DECIMATE 60 ${MOVEKWD30} 27
END
TSF EDIT SIN
SIN 1.0 ${SINFRQ:[0.0805114]} 0.0
FILTER D:WD KAIS 40 2.1 0 0.05 1.0 0.0
DECIMATE 10 ${MOVE} 0
FILTER D:WD KAIS 58 2.1 0 0.0333 1.0 0.0
FILTHR TAPRL=31 R t/urtap.prl]
DECIMATE 30 ${MOVEKWD30} 27
END
tslist _259200 -B -N -rs1. -Eprf.tse,SIN -qm -IThe -qm option gives us the min and max of the output, the FILTHR command the response of the second stage to a number of tides.
`setenv FRQ = `calc -f "%15.10f" '3600*0.05-0.0805114'and synthesize the following signal in prf.tse,SIN :
SIN 1.0 0.0805114 0.0Result:
SIN 1.0 ${FRQ:[179.9194886000]} 0.0
sasm02 -f WD KAIS 40 2.1 0 0.05 0.5 0.0

sasm02 -f WD KAIS 40 2.5 0 0.035 0.5 0.0
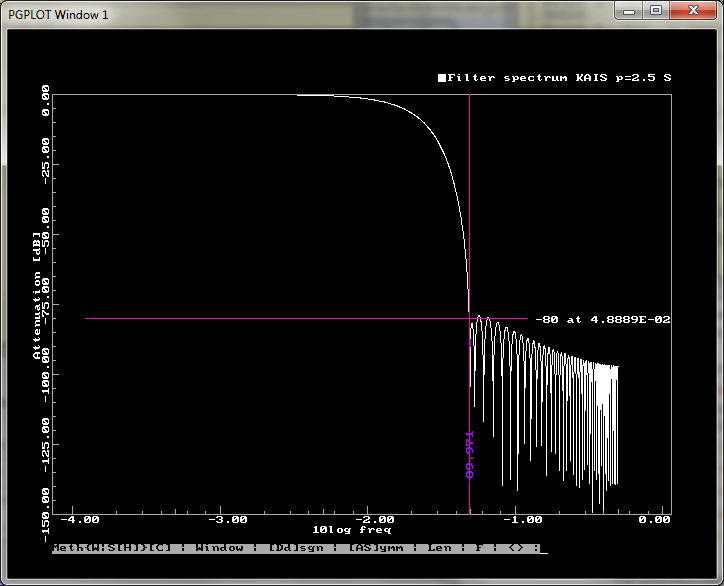
sasm02 -d8192 -f WD KAIS 240 2.5 0.0 0.0025 0.5 0.0
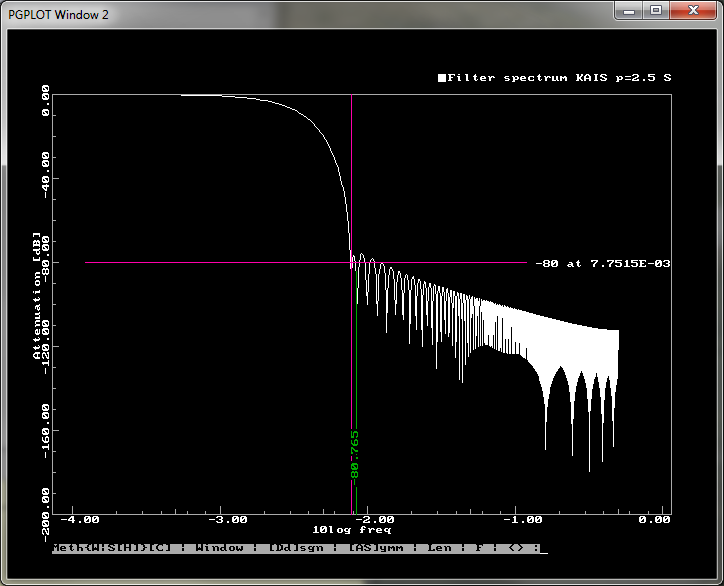
TSF EDIT C600STSF EDIT from 1s to 1h with a three-stage cascade
; first record out will be at 00:50:00
FILTER D:WD KAIS 40 2.5 0 ${UBE:[0.013]} 0.5 0.0
DECIMATE 10 ${MOVE:[560]} 0
FILTER D:WD KAIS 240 2.5 0.0 0.0025 0.5 0.0
DECIMATE 60 ${MOVEKWD60:[0]}
END
TSF EDIT C1HThe filter series of the last stage have been saved in ~/TD/f (linked ~/Ttide/SCG/f ):
; first record out will be at 05:00:00
FILTER D:WD KAIS 48 2.5 0.0 0.039 0.5 0.0
DECIMATE 5 3272
FILTER D:WD KAIS 56 2.5 0 0.008333333 0.1 0.0
DECIMATE 12 0
FILTER D:WD KAIS 240 2.5 0 0.00833333 0.5 0.0
DECIMATE 60 0
END
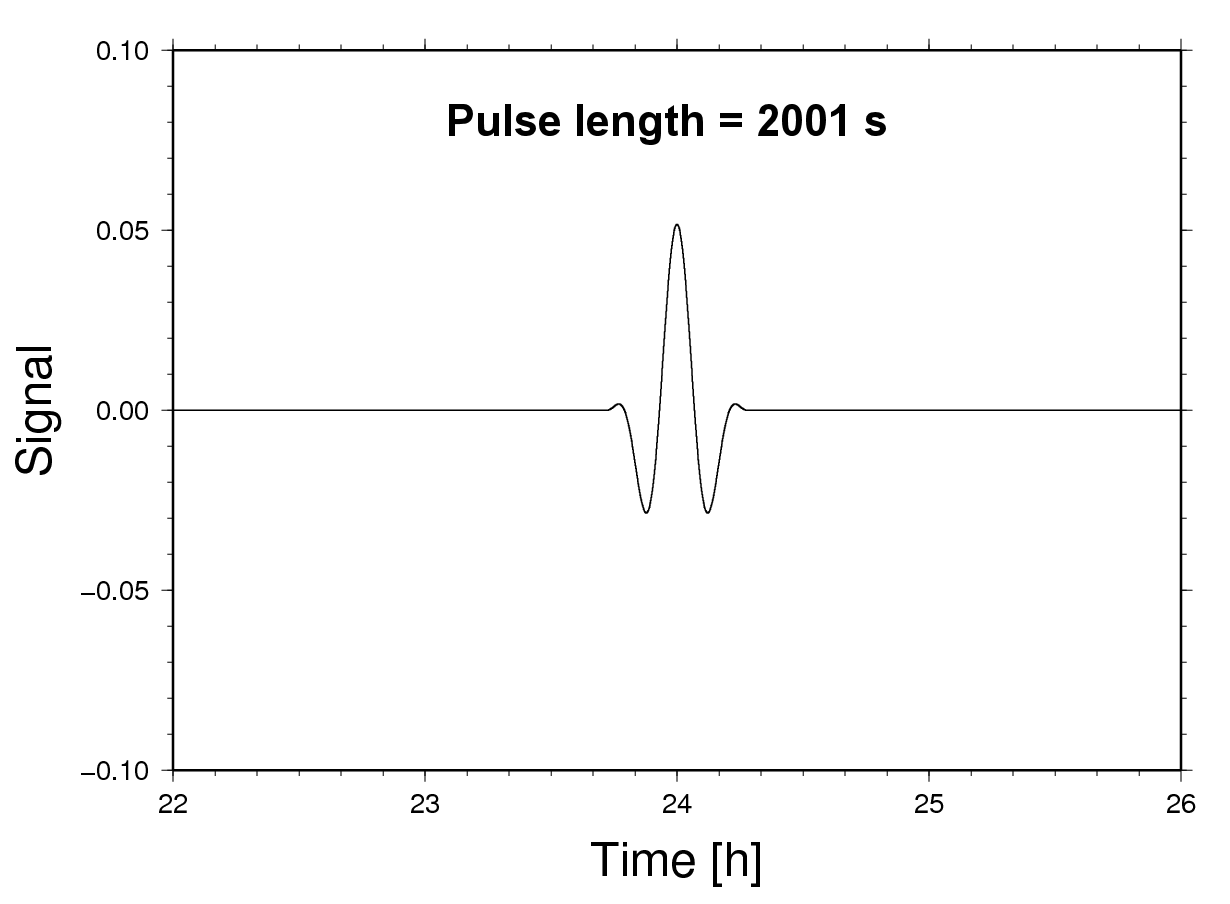
-rw-rw-r-- 1 hgs hgs 2033 Oct 31 00:35 f/WD-KAIS-240-2.5-0.0025-0.5-600s.fsThere are plots showing pulse responses of the decimation schemes. If the pulse length reads 0, the pulse is a single spike. In all other cases, the pulse has a zero-mean. The lengths shown mean full pulse length (the parameter for generation a pulse designate the number of positive off-centre ordinates). The pulse generator is here: ~/sas/p/pulsegens.f , double precision function pulsegen (t,scale,lhwidth).
-rw-rw-r-- 1 hgs hgs 2033 Oct 31 00:39 f/WD-KAIS-240-2.5-0.00833-0.5-1h.fs
do i=-lhwidth,lhwidth |
 |
 |
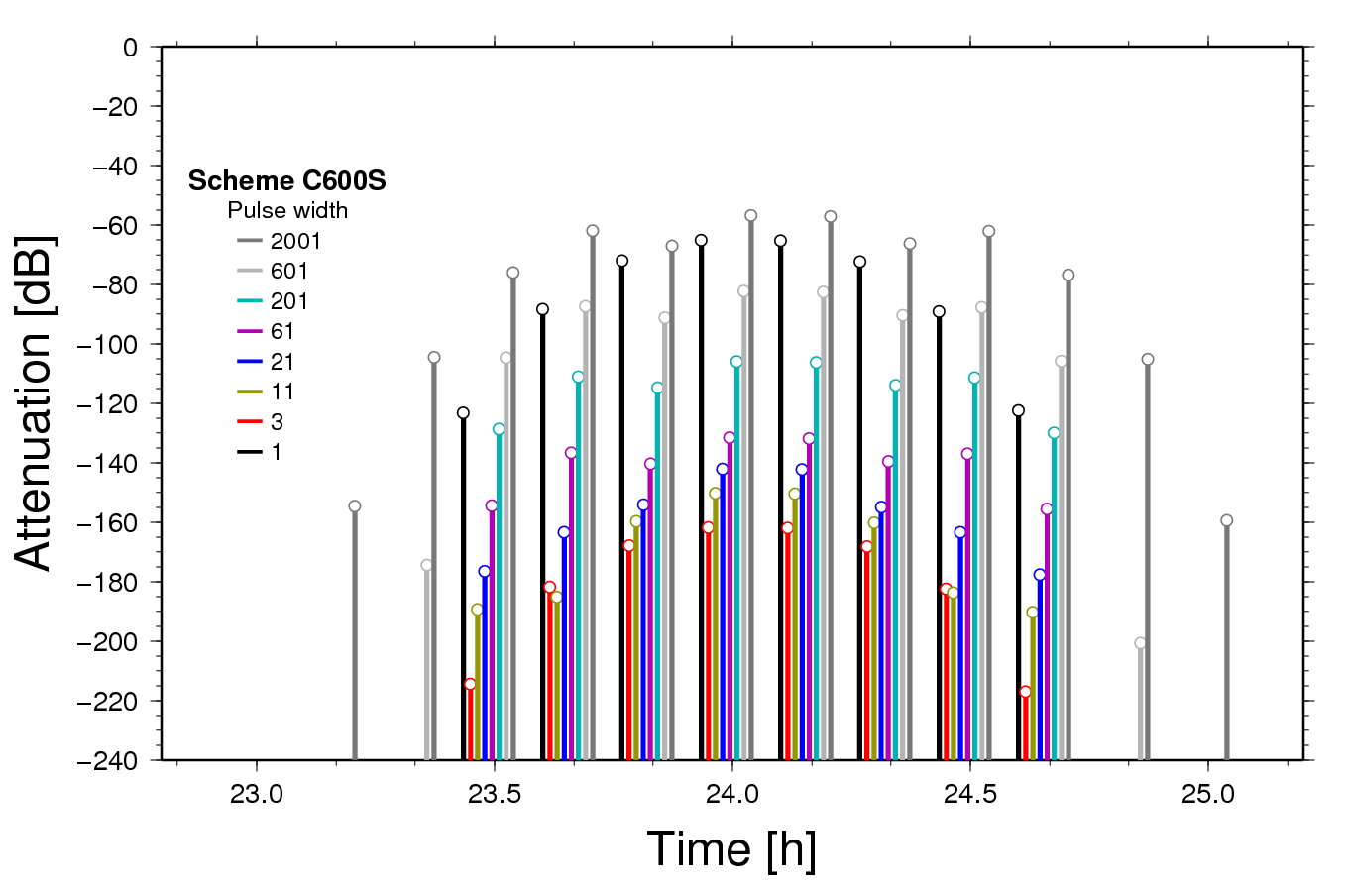 |
| Obs! that the longest pulse extrudes beyond the decimation filter length of the last stage. |
Nop = N (8 D1 +1 ) + N/D1 (8 D2 + 1 )Thus,
D1 D2 = Dtot
Nop = N (8 D1 + 1 ) + N/D1 (8 Dtot/D1 + 1 )In the number of operations (per sample of the input series times the filter scale)
Nop / 8N = D1 + 1/8 + Dtot/D12 + 1/(8 D1)we can neglect the last term. The minimum is found at
0 = 1 - 2 Dtot/D13or
D1 = cubicroot( 2 Dtot )
Dtot = 600 => D1 = 10.63
Dtot = 3600 => D1 = 19.31