We have a cycleslip subroutine directly callable from tslist (not: tsfedit).

#
# It can solve cycleslips in a time series by
# (1) improving the correlation to 1...m parallel time series
# (2) decreasing the variance of the series suspected for cycslips.
#
# Example AG drop residual and seismograph 3-D 100Hz data
# Z: sax
# E: svE N: svN
#
There are basically two superscripts, prepare and solve
prep-cycslips-problem
solv2-cycslip-problem

Prepare

The tasks are
(1) Provide the seismograms and their mutual correlations
(2) Set parameters

Before you know anything, the size of the cycleslip must be guessed:
 set csize = 10.0 # [uGal]
The strategy must be guessed (the T=-string):
 source prep-cycslips-problem sax raw SN T=0.0+S=1e10+W=0.25
(The "raw" means we prepare a job for the first time. We could recycle a cycslip solution, but this is done in a different way now)
The seismograms need preparation. Consult ~/Seismo/gcf/HOW.TO-gcf4ag
before you execute prepare.

You need a drop residual, which is the difference between AG-measurements and Superconducting gravimeter.

To obtain seimograph channel cross-correlation
 foreach ca ( E N Z )
  foreach cb ( E N Z )
   foreach ka ( sax sv )
    foreach kb ( sax sv )
     source any-any-corr $ka $ca $kb $cb 0 0
    end
   end
  end
 end
There are a number of default parameters in prep, of which you need to be aware of.


Solve

Here's the logic:
There is a range of parameters in this, so the procedure needs iterations.
In (7) outliers are iterated. Encircling (1) and (7), the drift parameter is iterated. These two iterations are automated.
In (6) you need a strategy; at least the weight factor in the penalty expression. Keyword STRATEGY
In (5) the filter order is needed. It's plausible with different lengths for saxZ on the one hand and svE/-N on the other. This step can be modified to produce predictions for a range of filter orders. Keyword MULTIPLE FILTERS
In (3) a clock offset is detected. (1)-(3) must be rerun, possibly again in a later pass, in order to ascertain the correct offset. Keyword: SHIFT
The whole procedure depends on the a-priori cycleslip size. Keyword: CSIZE

The reduction of RMS in step (7) may be used to judge whether prediction and cycleslip removal was satisfactory.
Hence, the iteration on the different parameters should always include step (7).

"Raw solution"
  set prev_agdrift = `get_prev_agdrift`
fetches the drift parameter from solold/ag-postlinpred.prl by default.
  set seishifts = ( +005 +005 )

 source solv2-cycslips-problem D
check the correlation offsets. The Z.correlogram should peak at lag 0. If not, enter S (makes solve stop), compensate by setting seishifts accordingly and rerun
If o.k., enter G
If you're sure the shifts are o.k., run next time with
  source solv2-cycslips-problem DG
If you want to fix the drift at the SG value, use
  source solv2-cycslips-problem DGU

 Stepping through filter lengths:
Make the predicted series
 source predict.env M

Analyze; either run with
  source solv2-cycslips-problem DGM[U]

or (edit/study the superscript and) run 
  cycslips-urtap-superscript
employing  cycslips-urtap.env  in a loop (the subdirectory where the urtap-prt files are collected in  soldir/mfo;
cycslip-urtap.env  will create it).

"Iterated solution"
 source prep-cycslips-problem sax 0 SN T=0.0+S=1e10+W=0.25
 source solv2-cycslips-problem DG[U]

Plots

Generated on the fly: solnew/plot/ cross-correlations and linear prediction variance
linpred-var.ps
linpred-varZ.ps
saxZ-ag-CYCZEN.corr.ps
svE-ag-CYCZEN.corr.ps
svN-ag-CYCZEN.corr.ps

Histograms:
script: source ./histogramplot
result in  solnew/plot/postlinpred.ra-h.ps

Analysis of filter length
The data files are urtap protocols from which the post-fit RMS is to be extracted and plotted versus e.g. filter lengths
The E,N-lengths on the one hand (they are supposed to be the same) and the Z-length as the X- and Y-variables against the postfit RMS
or the RMS gain (post/pre) by colour.
Prerequisits:  source predict.env M  and  cycslips-urtap-superscript

 set anyprl = `ls solnew/mfo/c$csize-* | head -1`
 set prerms = `awk '/preRMS/{print $2}' $anyprl`
 set stratmsg = "Strat.: T=0.0+S=1e10+W=0.25"
 set slipmsg = ", Cycleslip = $csize"
 awk -v p=$prerms '/PostRMS/{print $4,$6,p/$2}' solnew/mfo/c$csize-*.prl >! rmsgain-lh-lz.xyz
 awk '/PostRMS/{print $4,$6,$2}' solnew/mfo/c$csize-*.prl >! rms-lh-lz.xyz
 makecpt -Chaxby -T#datamin/#datamax/#datastep >! rmsgain.cpt
 makecpt -Chaxby -T#datamin/#datamax/#datastep >! rms.cpt

 set xl=10 xu=70 yl=5 yu=55 xs=a10f1 ys=a10f1
 set xtit="Pred.Filter Length E,N"
 set ytit="Pred.Filter Length Z"

 set psout = $plot/rmsgain-lh-lz.ps
 pscontour rmsgain-lh-lz.xyz -X2 -Crmsgain.cpt -JX6/6 -R$xl/$xu/$yl/$yu -I \
   -B${xs}:"$xtit":/${ys}:"$ytit"::."RMS gain vs PFL":WeSn -K > ! $psout
 psscale -D6.5/2.5/5/0.5 -Ba0.1f0.01 -Crmsgain.cpt -O -P -K >> $psout
 pstext <<EOF -N -O -R0/1/0/1 -JX6/6 >> $psout
 0.98 1.02 12 0 0 3 Strategy: $stratmsg$slipmsg
EOF

 set psout = $plot/rms-lh-lz.ps
 pscontour rms-lh-lz.xyz -X2 -Crms.cpt -JX6/6 -R$xl/$xu/$yl/$yu -I \
   -B${xs}:"$xtit":/${ys}:"$ytit"::."RMS vs PFL":WeSn -K > ! $psout
 psscale -D6.5/2.5/5/0.5 -Ba0.1f0.01 -Crms.cpt -O -P -K >> $psout
 pstext <<EOF -N -O -R0/1/0/1 -JX6/6 >> $psout
 0.98 1.02 12 0 0 3 Strategy: $stratmsg$slipmsg
EOF


Analysis of cycslip size and weight
cycslips-urtap-cw-superscript
awk '/Var-weight/{w=$6} /preRMS/{p=$2;c=$3} /PostRMS/{o=$2;print c,w,p}' solnew/moo/*-f023-023-035.prl > ! varcw-prerms.xyz
awk '/Var-weight/{w=$6} /preRMS/{p=$2;c=$3} /PostRMS/{o=$2;print c,w,o}' solnew/moo/*-f023-023-035.prl > ! varcw-postrms.xyz
awk '/Var-weight/{w=$6} /preRMS/{p=$2;c=$3} /PostRMS/{o=$2;print c,w,p/o}' solnew/moo/*-f023-023-035.prl > ! varcw-rmsgain.xyz



From here on, the text is old

We use the AG drop residual which is common in each saxdata or svdata file. We could also use
svdata/ag-dropres.ts (no label)

# Find optimum cycle slip size, weight, threshold (always "weak strategy"):
vary-cycslips DCWPPP -r -10,10 -n -g 30 -n -s 1e10
vary-cycslips DTWPPP -r -10,10 -n -c 11.0 -s 1e10
vary-cycslips DCTPPP -r -10,10 -n -g 30 -w 0.2 -s 1e10



At this time we have two strategies for cycle slip determination, strong or weak.
Strong is invoked with the option +S, e.g.
 -CYCSLIP${s},-3,3,T=0.+S,O#51:cycsl-ZEN.dat
and does not merit the decrease of variance

This is a strategy string for -CYCSLIP that was used with some success
 T=0.0+S=1e10+W=0.2

# this is done with
source prep-cycslips-problem sax raw SPPPN T=0.0+S=1e10+W=0.2

# the sampling of the slip size must be set in vary-cycleslips hands-on
Examples that vary-cycslips may provide

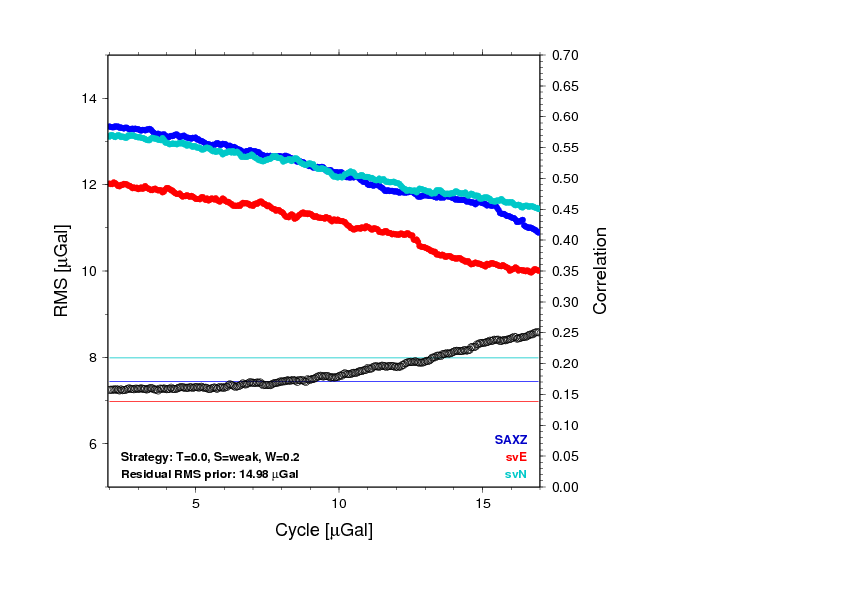
Example 1: Regularly made by prep-cycslips-problem


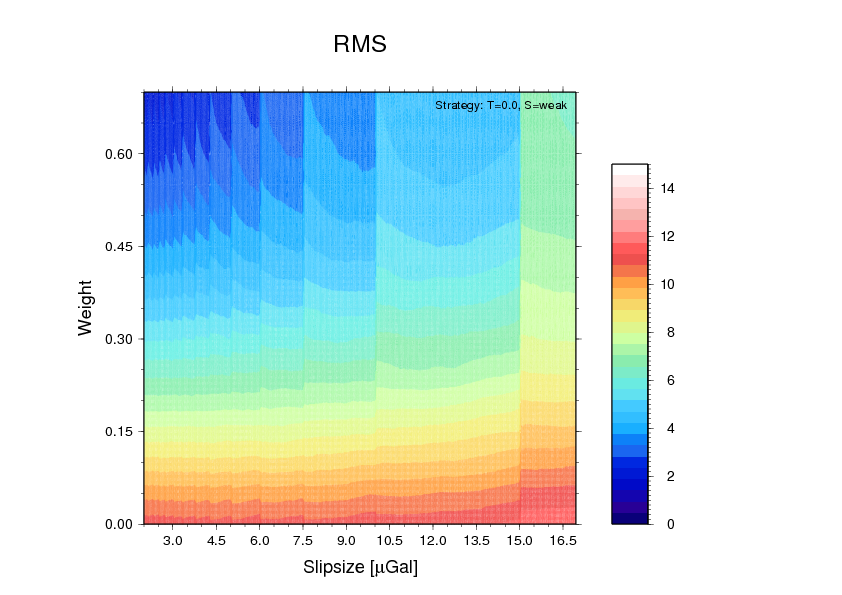
Examples 2 (left):  plot/PNG/cycslip-CW-RMS-T=0.0+S=1e10+W=0.7.png and 3 (right): cycslip-CW-CORRE-T=0.0+S=1e10+W=0.7.png
from vary-cycslips DCWPPP -r -15,15 -n -g 30 -n -s 1e10
provides the RMS (colour) and Correlation coefficient (abs value), respectively, as a function of weight and slip size.



The basic ambition is to
(1) remove cycleslips to increase correlation with seismograms
(2) find a prediction filter to decrease a seismic influence on the drop scatter; predict and obtain a residual
(3) subtract the prediction from the original series, obtain a drift term, and go back to (1) to adjust cycleslips in those samples that got a wrong slip
(4) when the drift term has stabilised, subtract the iterated slip series from the original series and compute a new prediction filter.
(5) obtain the residual and plot histograms: (a) The original series minus the predicted seismic effect, (b) the residual, (c) the original series minus the cycle slips. 

The process is divided into three parts
(P1)  Compute the corss correlations between the different seismic channels:  svE-svE-gm.corr ... saxZ-saxZ-gm.corr
        using any-any-corr
(P2) Prepare = find out a viable set of csize, weight and threshold = strategy
        using prepare-cycslips-problem
(P3) Solve
        using solve-cycslip-problem
        The solve-stage iterates the drift parameter and produces a time series of slips. Solve should be iterated, since the particular
        slip series will have an effect on the prediction filter. In the next round, we use the predicted series to - hopefully - make the slip
        events better detectable. By iteration, we hope for a convergence of the slip series and the prediction filters.

For (P2) and (P3) there is a superscript which steps through a range of slipsizes
#!/bin/csh
foreach csize ( 8.0 8.5 9.0 9.5 10.0 10.5 11.0 11.5 12.0 12.5 13.0 )
source  prep-cycslips-problem sax raw S T=0.0+S=1e10+W=0.2
source solve-cycslips-problem $1
foreach vnr ( 0 1 )
source  prep-cycslips-problem sax $vnr S T=0.0+S=1e10+W=0.2
source solve-cycslips-problem $1
end
end
exit


Use
superscript DH
where D requests recomputation and H histograms. The strategy is hard-wired

(P1):
The following five jobs are needed:
source any-any-corr sv N sv EN -005
source any-any-corr sv E sv EN -005
source any-any-corr sax Z sv EN -004 -005
source any-any-corr sv E sax Z -005 -004
source any-any-corr sv N sax Z -005 -004
source any-any-corr sax Z sax Z -004

The pre-requist that this all works is detailed in ~/Seismo/gcf/HOW.TO-gcf4ag

(We should have it as an html)
(The prep-and-solve steps need detailed documentation; they generate a bunch of files in a whitful set of subdirectories)
.bye