OTEQ - General information

back to TOP level

OTEQ = Ocean Tide EQuations

The hydrodynamic differential equations of the tides and storm surge problem
are solved using a finite difference method with constant time step and constant
spatial step widths.

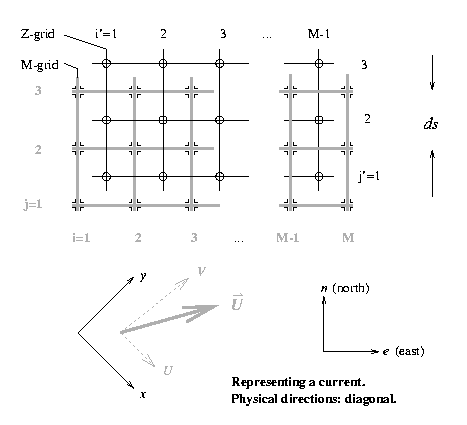
The spatial domain is a flat earth approximation with some (hopefully the
most important) earth spherical effects or consequences of geometry being
mapped. The different fields are gridded (discreteized) in a special fashion
following the work of Sielecki (1968) and Wübber and Krauss (1979).

Mapping is by stereographic projection. Procedures are available at
/home/hgs/OTEQ/s/oteu011.f
 

Discreteization of space.

Since the tide equations consist of two+one coupled first order differential equations
in both time and space, staggered grids are a natural choice.
One grid on which the currents are represented is interleaved with the
elevation grid.

The fundamental directions in a physical sense (x,y) are along the diagonals of the grids.
The grid representing the currents is given the type code M, the one for elevation the type
code Z.  The Z-grid has one row and one column less than the M-grid. However, for
file reading/writing we will input/output MxN elements, though there will be M+N zeros
when we process a Z-grid.

Ocean depth, currents (and eventually surface wind) are represented on the M-grid;
elevation, tidal gravity potential (and eventually air pressure) on the Z-grid.

In the scientific texts we can distinguish the two grids by unprimed and primed index
numbers, i.e.  i,j  on the M-grid and  i',j' on the Z-grid.

The position of a grid point from the origo (centre of the area) in kilometers e - east
and n - north is given by

e = [i-(M+1)/2]*ds,   n = [j-(N+1)/2]*ds    (M-grid)

e = [i'-M/2]*ds,         n = [j'-N/2]*ds            (Z-grid)

where  ds  is the grid constant. In the programs it is usually termed  SCALE and its
numerical value is given in kilometers.
 
 

Discreteization of time

Typically a suitable spatial step width (ds) is selected first. A critical time step
(dtcrit) is derived from ds and the maximum depth of the area using a
Courant-Levi-Friedrichs condition. The actual time step is then selected
using dtcrit  as an upper bound and adjusting dt to obtain an integer division
of a tidal cycle. The principal lunar tide M2, for instance, has a period of
44,714.165 s. If  dtcrit  is e.g. 47.0 s, the tidal cycle is integer-divided by  dt=46.9687 s
into 352 steps.
 

How the flags work

The solver for the differential equations as well as a number of routines for data retrieval
and graphic display need guidance as to the conditions prevailing at a geographical point
of interest (at a grid node). One has to distinguish for instance whether a grid node represents
sea, land, out-of-area, active boundary or passive boundary.
The M- and the Z-grids are represented by one flag array each.

Flag values may show three things:
(1) represent a circumstance (e.g. land/sea)
(2) indicate a specific kind of boundary condition
      (e.g. a straight piece of shoreline running north-south
       with sea to the east)
(3) specify a storage address for memory-efficient storage of
      auxiliary data (mostly the tide height along an open boundary)

Some basic facts:
Passive boundary conditions are associated with land.
Passive boundary conditions apply only to the equation of the currents.
Out-of-area nodes need only a distinction between land and sea.
An active (open) boundary is associated with sea.
Passive boundary conditions may occur on the end members of a
   segment of active boundary, where it eventually touches land.
Using open boundaries a model can be driven by elevations or
   currents or a combination (compatibility needs to be established though).
   The boundary current case, however, is rare since such data is usually rare
   or uncertain or noisy.

See more under  Passive boundaries  or  Other flags.

Job tasks

The tasks can be divided into four categories
 
  1. Create a model (CREAM), program name  cream, document name  /home/hgs/OTEQ/DOC/prep.doc. Code is available at /home/hgs/OTEQ/PREP/cream.f
  2. Prepare tidal gravity potential and other tide-specific information. Two programs to be run after one another, named  otem92  and otem16, document names prep2.doc  and  otem16.doc . Code is available at /home/hgs/OTEQ/PREP/otem92.f and /home/hgs/OTEQ/PREP/otem16.f
  3. Do the modelling. Subtasks: Tides, Pressure, Wind excitation, Static pressure loading.
  4. Post-processing of various kinds.

    5.  

     
     

    Tide excitation: Recommended program has name  otemt1, document names  otemt1.doc  and    otet.doc.  Code is available at geo/hgs/PC/OTEQ/EXEC/otemt1.f

    Pressure and wind excitation: Recommended program has name otemw1.  Code is available at geo/hgs/PC/OTEQ/EXEC/otemw1.f

    Static pressure loading: Recommended program has name apload. Code is available at geo/hgs/PC/OTEQ/EXEC/apload.f
     
     

Data Files

Most data is written binary in order to save space. This causes a need to provide tools to inspect the files so the user can evaluate the success of programs.

See the pages about general aspects of files and displays.
 

.bye