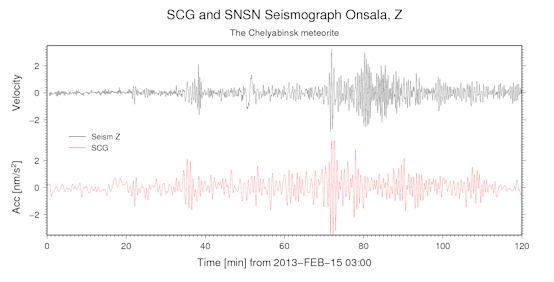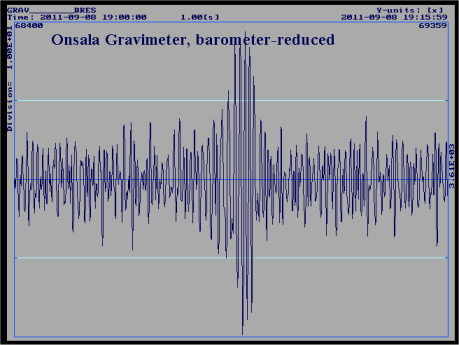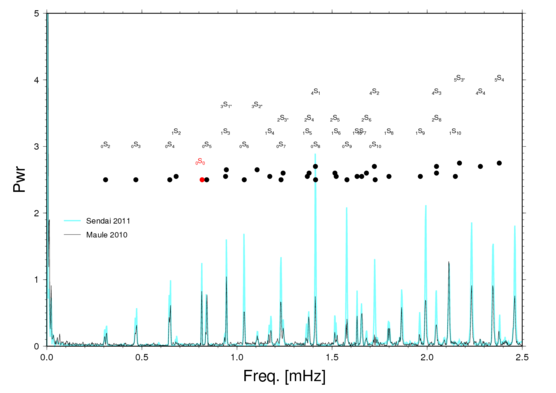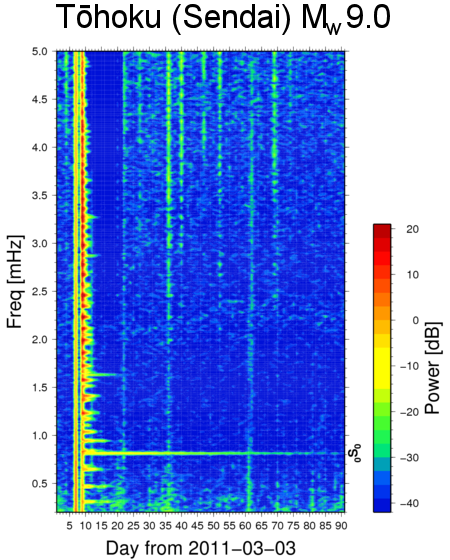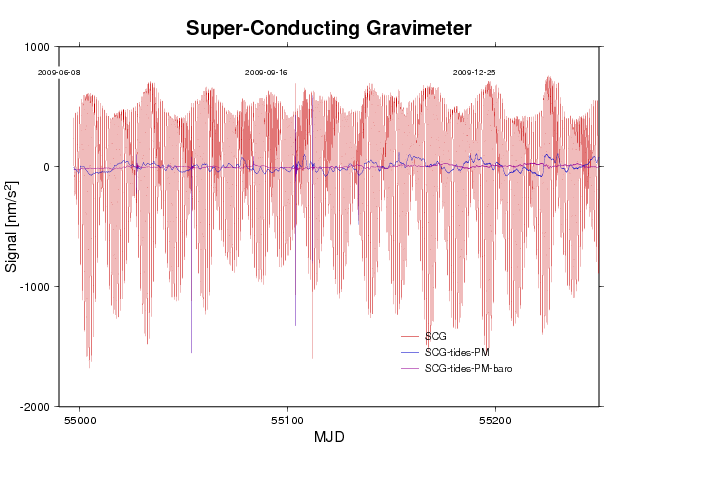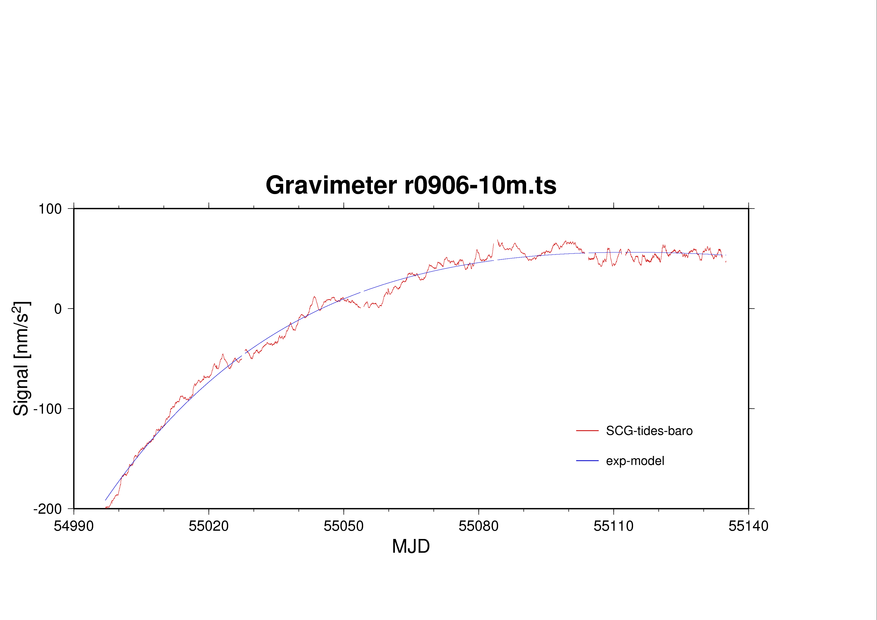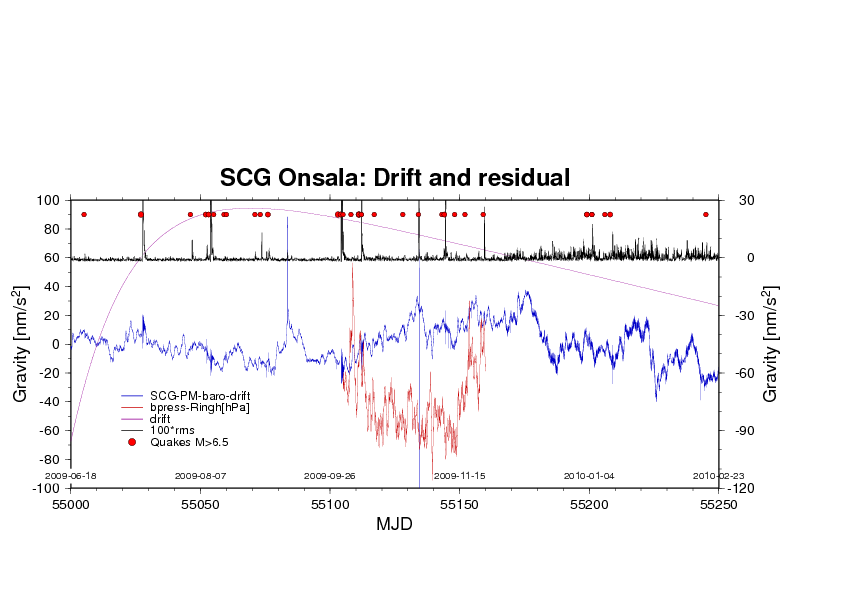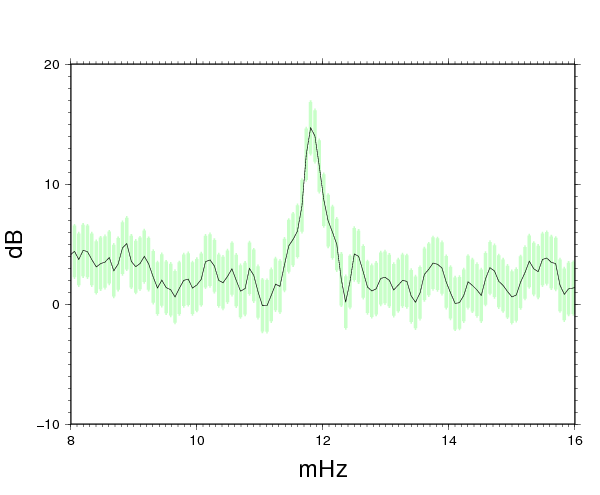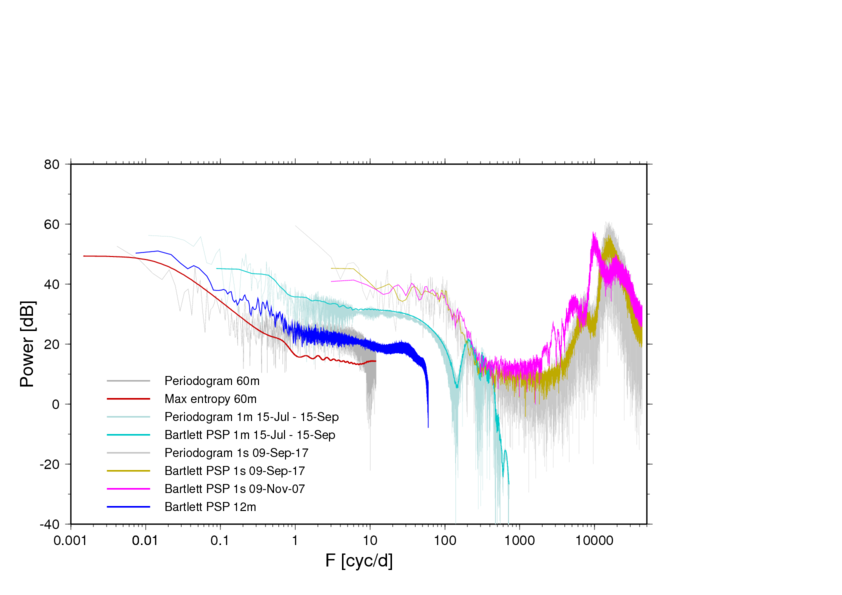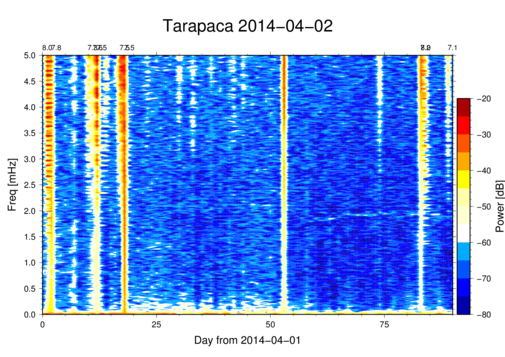
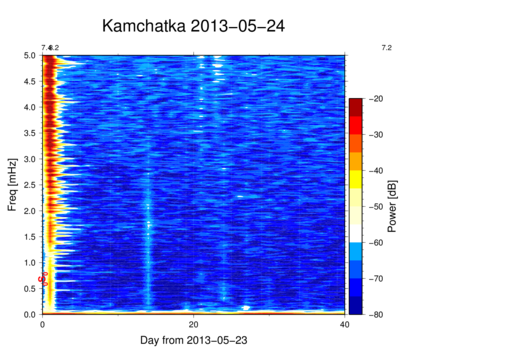

Automatically updated every morning 8 a.m. (click on image to show full size). Temporal resolution is one day. Estimated from 15-s data, thus frequency resolution is 0.011574 mHz. Although this resolution is not optimum for detection of the 0S0-mode (0.81699 mHz), the use of a Hanning window warrants enough amplitude response to make the signal visible.